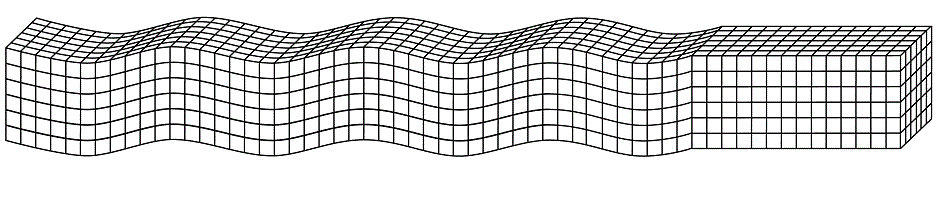
Этим постом открывается цикл заметок о моделировании сигналов ультразвуковых дефектоскопов численными методами. В них хотелось бы в неформальном стиле описать решаемые задачи, предположения и предварительные выводы, полученные в результате расчетов.
Зачем все это надо? (Моделирование-1)
В ультразвуковой дефектоскопии основным критерием отбраковки является превышение эхосигналом какого-то порогового значения. Значения эти обычно настраиваются непосредственно перед контролем по образцам, принятым в данной отрасли, и потому вопрос связи амплитуды сигнала с его размером и положением носит абстрактно-теоретический характер. Нормативные документы множились, появлялись новые эталоны, как-то связываемые со старыми. Постепенно это привело к тому, что из-за накопившейся ошибки один и тот же норматив при контроле может требовать разных уровней сигнала. При этом простого решения нет: Со стороны теории формулы имеют очень приблизительный характер и существенно расходятся с практикой. Впрочем, это не удивительно – до недавнего времени особой потребности в них не было. Практические же измерения, в отличие от толщинометрии, не дают нужную стабильность результатов, так как малейшее изменение прижима, шероховатости и т.п. тут же отражается на амплитуде. Это была первая проблема.
Вторая связана с появлением нового класса приборов – дефектоскопов с фазированными антенными решетками. Их возможности могут существенно различаться в зависимости от используемых алгоритмов. Но всех их объединяет то, что на экране они показывают не сечение объекта, а акустический образ этого объекта. Принципы же формирования этого образа часто не очевидны, а иногда и вовсе неизвестны.
Значит, требуется какое-то средство, позволяющее понять, что именно происходит с акустической волной внутри твердого тела, и как-то определить ее параметры. Так как за последние 50 лет аналитических формул, описывающие нужные нам закономерности, так и не появилось, логично предположить, что вывести их невозможно. Остаются численные методы. В этой области все обстоит относительно неплохо. Метод конечных разностей во временной области (FDTD), разработанный первоначально для электромагнитных полей, был уже давно адаптирован для расчета упругих волн. Хорошо проработаны методы оценки его устойчивости, граничных условий и т.п. Но есть у FDTD существенный недостаток - он крайне требователен к вычислительным ресурсам. По грубой оценке, прохождение волны от стандартного преобразователя в стальном кубике с ребром в пять сантиметров потребуется считать где-то неделю. На мощном персональном компьютере образца 2014 года. Остается только капать слюной, читая отчеты о том, как сейсмологи моделируют волны этим методом на вычислительных кластерах с полутора тысячами ячеек по восемь ядер в каждой. Что делать – неразрушающий контроль отрасль бедная.
В принципе, неделя на расчет не так уж и страшно. Да и дополнительную технику можно задействовать. Но для этого должна быть уверенность в том, что считается именно то, что нужно. А пока остается пробовать различные упрощения модели и смотреть, что важно, а что не очень. Ведь отладить работу численного метода очень сложно, несмотря на то, что его базовые алгоритмы обычно просты. Дело в том, что данные одной точки ничего о правильности работы не говорят, а все странности итогового результата нужно искать в свойствах математической2 модели. Хорошо когда есть несколько аналитических формул, дающих абсолютно точный результат. А если мы как раз хотим проверить точности общепринятых формул? Тут есть риск впасть в другую крайность, принимая собственные ошибки за гениальное ниспровержение основ. За последнюю неделю мне удалось разобраться в причинах двух таких “открытий”.
К чему все это? Во-первых, в процессе работы появляются любопытные результаты, которые могут кому-то пригодиться. Мне пришлось потратить немало времени на то, чтобы выяснить несколько “очевидных” тонкостей, которые посчитали ненужным указать в статьях. Во-вторых, выкладывая свои идеи в широкий доступ, строже относишься к их проверке. В-третьих, материал все копится и копится, я постепенно начинаю путаться в нем, а в хорошую статью он пока не отливается. Так что буду выкладывать здесь что-то вроде рабочих записок.