Написать эту заметку меня заставила очередная порция отчетов о лабораторных работах. Значительная часть графиков, приведенных в них, показывает, что многие студенты не понимают, что именно и зачем они делают с их помощью. Попробуем с этим разобраться, а заодно рассмотрим на реальных примерах как надо, а главное, как не надо их оформлять.
Итак: график, это способ наглядно представить численные данные. Ключевых понятий два: наглядно и численные данные.
Что в нашем случае "наглядно"? График это не просто замена таблицы, это способ выразить какую-то идею. Именно этой идеи и должно быть подчинено его оформление. При этом представленный результат должен быть достаточно лаконичным (не нужно загромождать графики лишней информацией), но содержать при этом все необходимое. В сложных случаях выбор вида графика может занять у специалиста не один день, а сам он превращается практически в произведение искусства.
Теперь поговорим о численных данных. Так как график является их представлением, то он должен делать это точно и однозначно. Как по таблице можно построить график, так и по графику должна быть возможность составить таблицу. Этим он и отличается от эскиза, показывающий примерный вид зависимости.
Какими способами студент XXI века может изготовить график?
- Воспользоваться компьютером и распечатать результат на принтере. Теоретически это самый простой путь, дающий наилучший результат. На практике, даже в этом случае можно сделать множество ошибок.
- Начертить график прямо на листе с отчетом. Для этого желательно иметь рейсшину или как минимум угольник и умение ими пользоваться. Кривое нечто, нарисованное ручкой, без линейки, за пятнадцать минут до сдачи, ничего кроме раздражения вызвать не может.
- Миллиметровка (при определенной аккуратности можно обойтись клетчатой бумагой) традиционный способ получить красивый график без особых хлопот. Все что потребуется кроме нее самой - линейка и карандаш. К сожалению, некоторые студенты считают, что миллиметровка обладает волшебным свойством, превращающим, в глазах преподавателя, кривые закорючки в ровные линии.
Перед построением графика нужно определиться с его размером. Выбирайте его исходя из числа точек, по которым вы будете его строить и необходимой точности. Графики, которые мы будем строить на лабораторных простые, половины листа А4 для них, пожалуй, будет многовато. И уж точно не стоит делать их меньше 5 см. На мой взгляд, оптимальный размер 10 см по большей стороне.
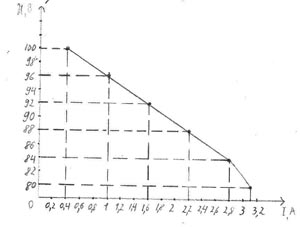
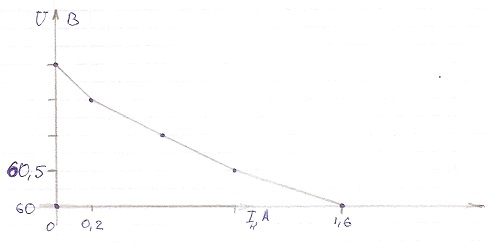
После этого нужно выбрать диапазон значений для осей. Если результаты изменяются в небольших пределах, то именно эту часть и нужно показать на графике. Вот два примера из отчетов об одном и том же опыте. На левом все точки сжаты по вертикали практически в одну, а на правом диапазон выбран верно. Это позволяет нам, несмотря на огромное количество других ошибок, сопоставить график со значениями в таблице и, если потребуется, вычислить промежуточные значения.
После выбора диапазона и масштаба нужно обеспечить необходимую точность. Из графика должно быть видно, что каждая обозначенная точка соответствует своему численному значению, а разметка осей должна позволять получить промежуточные значения.
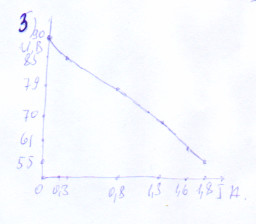
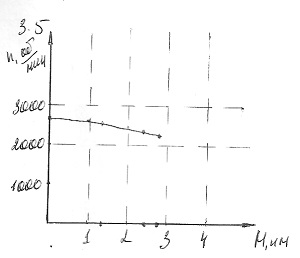
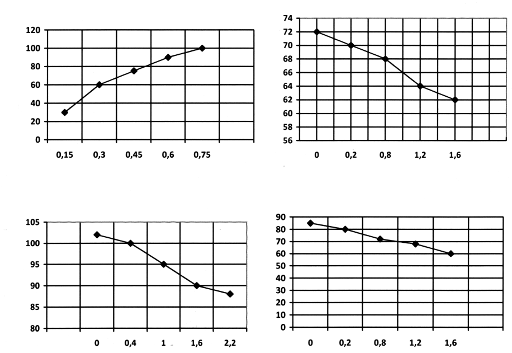
В точность вот этих графиков я не верю:
А вот эти похожи на правду, хотя на втором и поленились обозначить все значения на осях:
Важно не забывать подписывать не только размерности осей, но и сами графики. Далеко не всегда можно понять, что на нем изображено. Вот пример головоломки, полученной от студентов:
А вот пример из хорошо оформленной работы, которую легко и приятно проверять:
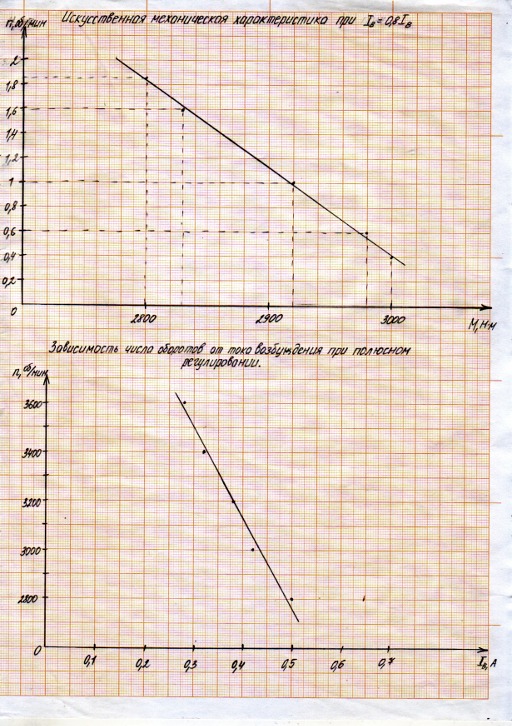
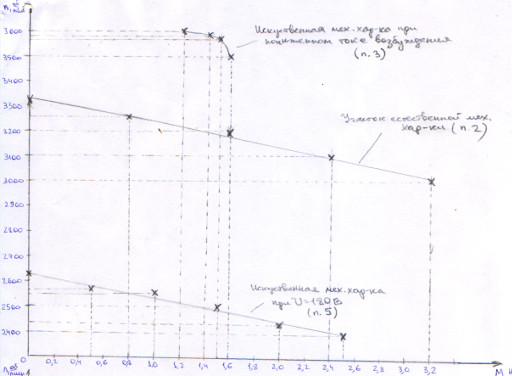
Если у вас получается несколько однотипных графиков со схожими диапазонами, лучше их объединить в один. Это повысит их наглядность и позволит сопоставить их друг с другом. Важно в этом случае не забыть указать какая линия чему соответствует. Хорошо это сделано на приведенном ниже примере:
Хотя верхнюю зависимость стоило все же сделать на отдельном графике, так как она сильно выбивается из общего масштаба.
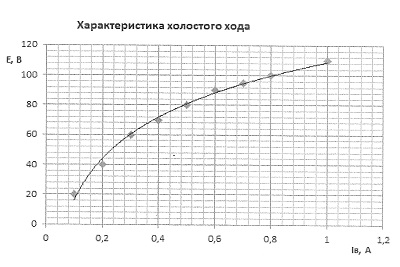
Сложный вопрос интерполяция графиков. Хорошо, если зависимость линейная и все точки легли точно. А если нет? Если вы знаете примерный вид зависимости, можно интерполировать их соответствующей кривой. В этом случае удобно использовать функцию "построить линию тренда" в MS Excel. Тогда можно получить что-то вроде этого:
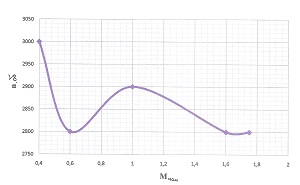
А вот такой график для линейной зависимости явная ошибка:
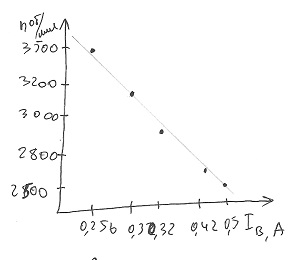
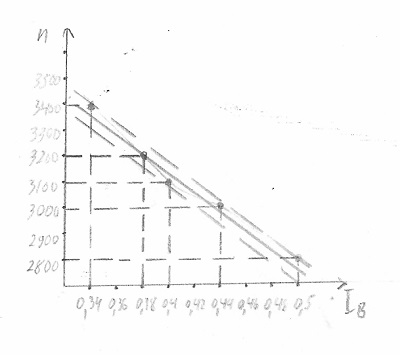
Очень порадовал студент, сделавший правильную интерполяцию графика и указавший интервал разброса точек. Сразу видно, что человек хорошо понимает, что и для чего он делает:
Продолжение следует.