Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /var/www/u1725042/data/www/shearwave.ru/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /var/www/u1725042/data/www/shearwave.ru/wp-content/plugins/latex/latex.php on line 49
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /var/www/u1725042/data/www/shearwave.ru/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /var/www/u1725042/data/www/shearwave.ru/wp-content/plugins/latex/latex.php on line 49
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /var/www/u1725042/data/www/shearwave.ru/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /var/www/u1725042/data/www/shearwave.ru/wp-content/plugins/latex/latex.php on line 49
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /var/www/u1725042/data/www/shearwave.ru/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /var/www/u1725042/data/www/shearwave.ru/wp-content/plugins/latex/latex.php on line 49
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /var/www/u1725042/data/www/shearwave.ru/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /var/www/u1725042/data/www/shearwave.ru/wp-content/plugins/latex/latex.php on line 49
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /var/www/u1725042/data/www/shearwave.ru/wp-content/plugins/latex/latex.php on line 47
Warning: preg_replace(): The /e modifier is no longer supported, use preg_replace_callback instead in /var/www/u1725042/data/www/shearwave.ru/wp-content/plugins/latex/latex.php on line 49
Вот хороший пример очевидной, на первый взгляд, вещи, которая при более внимательном изучении оказывается не такой простой.
Что показывают нам в качестве единиц амплитуды дефектоскопы? Децибелы. А какие именно децибелы? Ведь, в зависимости от того, является величина энергетической или нет, используется коэффициент либо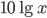 
, либо 
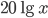. Дефектоскоп определяет сигнал по уровню напряжения, полученному с пьезоэлектрического преобразователя. Значит, нужно использовать "неэнергетические" 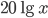. Пока все понятно.
А откуда взялось напряжение в преобразователе? Из-за прямого пьезоэффекта, который, если не вдаваться в детали устанавливает прямую связь между напряжением и приложенным давлением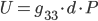 
Звуковое давление же у нас определяется по формуле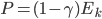 
. Получается, что напряжение в приемном тракте дефектоскопа прямо пропорционально энергии? Получается, что так. Значит, нужно использовать "энергетические" децибелы? Теоретически да, но по сложившейся традиции используют "неэнергетические".
А так как при моделирования волнового уравнения результат получается в виде скорости колебаний среды, которая связанна с кинетической энергией формулой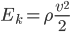 
, то для получения правильныл децибелов нужно брать уже 40 логарифмов скорости.
Вроде бы мелочь, но мне пришлось поломать над ней голову несколько дней, прежде чем я понял, почему расчетный график ВРЧ не совпадает с экспериментальным.